

|
Солнечно-земная статьи и доклады |
B.M.Kuzhevskij, O.Yu.Nechaev, M.I.Panasyuk, E.A.Sigaeva
Б.М.Кужевский, О.Ю.Нечаев, М.И.Панасюк, Е.А.Сигаева
Skobeltsyn Institute of Nuclear Physics of Lomonosov Moscow State University, Moscow, Russian Federation
Abstract.
Изучается распределение скорости счета тепловых и медленных нейтронов, регистрируемых из двух направлений: к земле и от неё, вблизи земной поверхности по экспериментальным данным, полученным в Москве, в 1996 году.
Получено, что математически данное распределение описывается суммой двух функций: распределением Пуассона и логарифмически нормальным распределением. Мы предполагаем, что логарифмически нормальное распределение описывает вклад земной коры в полный поток нейтронов. Обнаружена корреляция между случаями нарушения полученной формы распределения и изменениями в околоземном космическом пространстве (например, Лунными фазами и пересечением Землёй секторных границ межпланетного магнитного поля). Возможно, что изучение изменений в распределении нейтронов вблизи земной поверхности позволит прогнозировать космическую погоду.
Distribution of neutron counting rate near the Earth surface is studied in two directions - to the Earth and from it - according experimental data, obtained in Moscow in 1996. It results in a claim that full mathematical approximation of neutron' counting rate distribution is described by a sum of two functions: Poison distribution and logarithmically normal distribution. We suppose that logarithmically normal distribution describes an input of the Earth crust into the neutron flux. Found correlation between a breach of thermal neutron distribution and space condition and events (e.g., Moon phases and crossing of Interplanetary Magnetic Field sectors) gives us an opportunity to use these data for analysis and prediction of space weather.
The primary study of thermal neutrons near the Earth crust have shown that up to level of 2 km thermal neutrons’ density does not depend on altitude (Beliaeva et.al., 1999(a), Kuzhevskij et.al., 1996). So this region in the Earth atmosphere can be regarded as a neutron field, where time distribution of neutron fluxes in the neutron field of the Earth can be written as:
![]() (1)
(1)
where n(t) – is time distribution of neutron concentration in the neutron field of the Earth,
v –is speed of neutrons.Experimental studies of the energetic spectrum of neutrons near the Earth crust [Beliaeva et.al., 1999(b)] have shown, that over 70% of neutrons have energy below 0.5 eV. Observations of propagation of neutrons with primary energy less than 1 MeV have shown, that during a period shorter than 1 sec (a real value is about 0.1 sec) neutrons with such energies become thermalised and during a period shorter than 0.1 sec captured by atmospheric nitrogen [Kuzhevskij, 2000]. As a result in formula (1) neutron speed v is a mean speed and time variation F(t), will be defined by time variation of neutron density n(t) only. Real neutron measurements give us the neutron count rate
![]()
where S is detector area. Mathematical approximation of experimental data
![]() (2)
(2)
will be thus mathematical approximation of neutron density in the neutron field of the Earth. Analysis of this approximation allows us to study properties of neutron source and nature of this flux variations.
Earlier [Kuzhevskij et.al., 2001] it was found out that there seems to be as a minimum two neutron sources near the Earth crust. The first source is the generation of neutrons in the Earth's atmosphere as a result of interactions between high-energy space particles with nuclei of the Earth's atmosphere elements. The second source is radioactive gases (Radon and Thoron), which produce a
-particles with energies up to several MeV. These particles, in turn, generate thermal neutrons during interactions with the elements of the Earth crust and atmosphere. It also have been shown [Kuzhevskij et.al., 2001], that short-time variations of neutron flux result from dynamical processes in the Earth crust.
Careful studies of neutron intensity for a period 1993-1998 using epoch method have shown correlation between daily-averaged intensity of neutrons and Moon Phases. As it’s seen in
Figure 1, days of Full Moon and New Moon exhibit an evident growth of neutrons intensity.
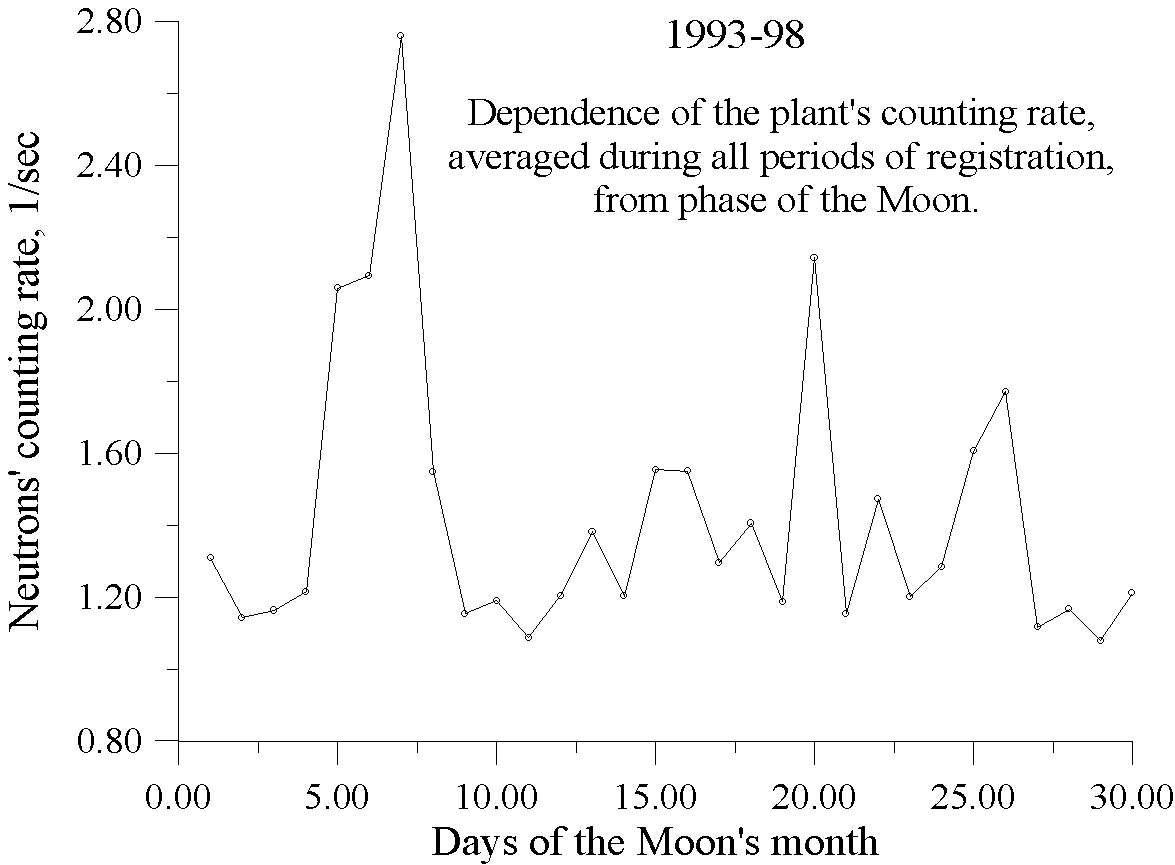
Figure 1. Information for 1993-1998 distributed according the Moon’s month after applciation of “epoch’s” method.
We have analysed count rates of neutrons in directions to the Earth crust and from it at the Earth level measured in Moscow [Kuzhevskij et.al., 2002] in 1996. The count rate distribution is described by sum of two functions: Poison function with parameters a1 and l and logarithmically normal distribution with parameters a2 and b.
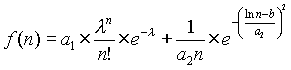 (3)
(3)
Poison distribution describes count rates up to 5 neutrons per second (it corresponds to neutron flux 2.5´
10-3 s-1cm-2), and logarithmically-normal distribution describes counting rate over 5 neutrons per second. It's necessary to note, that logarithmically normal distribution was obtained for count rates up to 15 s-1, but count rates up to 50 s-1 are successfully described by this function. Although sometimes we observed essentially greater values of count rates (100-200 s-1), such big values of count rates can be hardly used for approximation because of a very low probability of their observations.
For quiet periods (for which counting rate does not exceed 5 s-1) distributions can be successfully described by Poison distribution. Logarithmically-normal distribution is important in cases where counting rates exceed 10 neutrons per second. Such situation is unusual for quiet periods and appears mainly during disturbed periods (so called splashes). According [Kuzhevskij et.al., 2001] we selected disturbed periods as periods of registration, for which hourly-averaged values of neutron flux exceed monthly-mean more than 10% [Kuzhevskij et.al., 2002].
Studies of dependence of splash period durations on time of year show, that longer splashing periods are more characteristic for neutron flux propagating in direction from the Earth, than for neutrons propagating in direction to the Earth. Analysis of neutron distribution results in a conclusion, that long splashing periods are seasonally dependent.
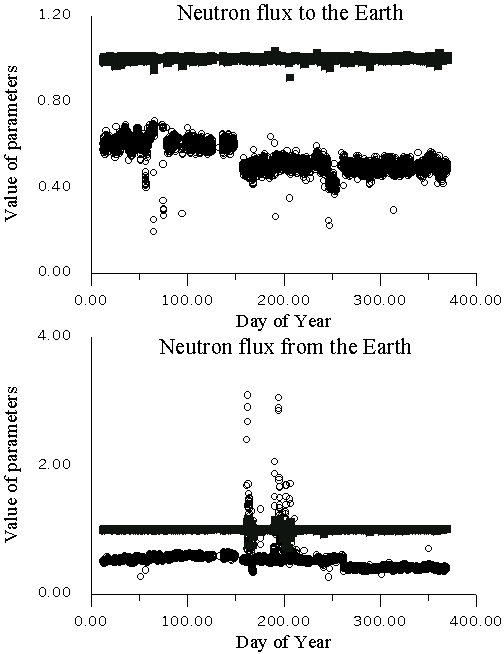
Figure 2. Seasonal dependence of approximation parameters a1 and l of Poison distribution, which describes distribution of quiet periods for neutron flux, directed to the Earth and from it. Black squares - parameter a1, circles - parameter l. Great amount of points for the neutron flux, directed from the Earth, in the middle of the year (150-200 DOY) corresponds with increasing of neutron fluxes from the Earth surface during this period. Because of it the average counting rate for this period increases.
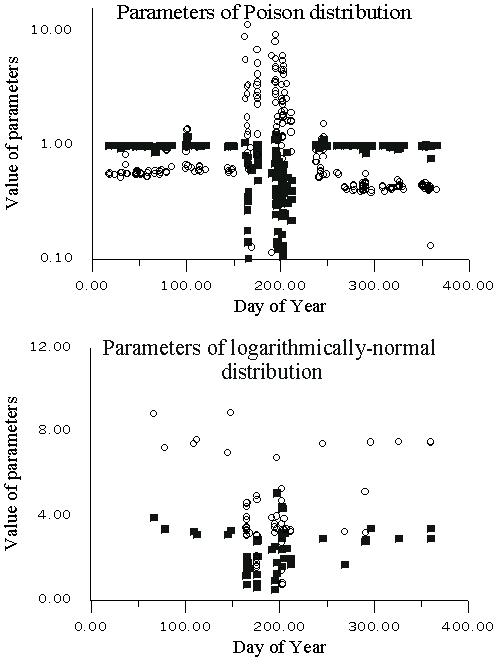
Figure 3. Seasonal dependence of approximation parameters, which describe distribution of splash periods for neutron flux, directed from the Earth. Upper axes - parameters a1 (squares) and l (circles) of Poison distribution, lower axes - parameters a2 (squares) and b (circles) of logarithmically-normal distribution. Great amount of points in the middle of the year (150-200 DOY) corresponds with increasing of neutron fluxes from the Earth surface during this period.
Changes of parameters included into formula (3) were studied. They are presented in Figure 2 for Poison distribution for quiet periods. In Figure 3, the parameters of Poison and logarithmically-normal distributions of neutron flux from the Earth surface are plotted for disturbed periods. The plots confirm that Poison distribution parameters do not change for quiet periods, but during disturbed periods they vary greatly (by a factor of ten). Figure 4 presents separate cases of full approximation of neutron count rates, which propagate to the Earth surface and from it, for disturbed periods. But there are also disturbed periods of registration, which can't be approximated in this way, i.e. they can't be presented as sum of Poison distribution (up to 5 s-1) and logarithmically-normal distribution (from 6 up to 15 s-1).
So we can grade the whole experimental sets for each direction of neutron propagation into different parts according to the type of approximation function. For more clearness we present this information in the following Table
Table
|
Usual periods (counting rate per hour does not exceed monthly mean value + 10%) |
Disturbed periods (counting rate per hour exceeds monthly mean value + 10%) |
||
|
"Short" distributions (less than 5 neutrons per second) |
|
||
|
"Long" distributions (more than 5 neutrons per second) |
Well approximated by sum of Poison and logarithmically-normal distributions |
Well approximated by sum of Poison and logarithmically-normal distributions |
Poorly or impossible to be approximated by sum of Poison and logarithmically-normal distribution |
Discussion
So, during the disturbed periods, especially for neutron flux directed from the Earth, approximation function contains two parts (formula (3)). Comparing experimental and theoretical data we came to the conclusion that the first part (Poison distribution) describes an input of high-energy space particles, which generate neutrons during interaction with nuclei of the Earth’s atmosphere elements. This part is almost invariable and does not depend on any processes. The second part of the approximation function is logarithmically-normal distribution, which plays an important role for disturbed periods with “long” distributions. This part describes input of the Earth crust. It varies greatly from one period to another depending on different processes in the Earth crust.
Therefore determined type of approximation function (formula (3)) confirms conclusion about important input of the Earth crust into the full flux of thermal and slow neutrons near the Earth crust, which was obtained by another method [Kuzhevskij et.al., 2001, Kuzhevskij et.al., 2002]. This function confirms that mainly this input of the Earth crust comes through during different types of splashes, which occur in the Earth crust (splash periods).
Figure 4. Examples of approximation of unquiet periods of registration for neutron flux from both directions.
Returning to Table, the most interesting cases for us in terms of study of space weather are those, whose approximation parameters differ strongly from an average value, or those, which are poorly approximated by sum of Poison and logarithmically-normal distributions. It was found out, that overwhelming majority of such events (over 90%) occurs on dates of the Earth crossing the border of sectors of Interplanetary Magnetic Field (IMF). Example of such event in neutron intensity is presented in Figure 5. Moreover, the rest events lay in a range of a day from such crossings. Because of poor accuracy of data about the Earth crossings boundary of IMF sectors (we operated only with dates of these events), these events also can be regarded as cases of correlation between changes of IMF sectors and splashes in thermal neutron distributions, which are impossible to be approximated by sum of Poison and logarithmically-normal distributions. Further we are going to make this study more exact, taking into consideration more accurate data of the Earth crossings boundaries of IMF sectors.
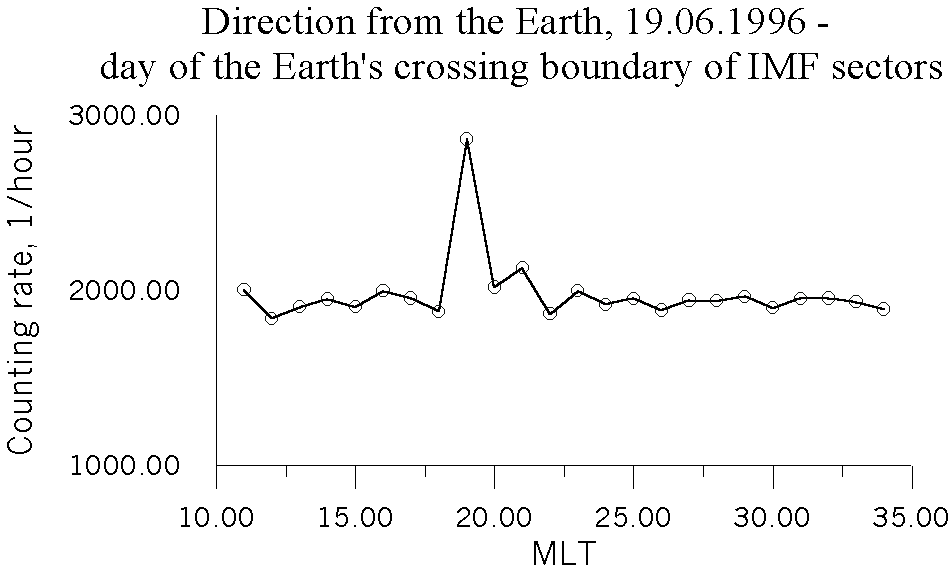
Figure 5. An example of increasing intensity of neutron flux from the Earth coincided with the Earth's crossing of IMF sectors boundary.
In order to explain this not obvious connection between the crossing of the boundary of IMF sectors and processes in the solid Earth it’s necessary to take into consideration that crossing such boundaries the Earth comes into magnetic field, which in turn generates alternating electric field. If we put a crystal into alternating electric field we’ll find changes of its overall size – it is a well-known reverse piezo-effect. So the microstructure of the Earth is deformed under influence of alternating electric field and it results in changes of neutron flux originated from the Earth crust.
At the same time Moon phases also correlate with “long” distributions of thermal neutrons near the Earth crust, but in 1996 there were no cases of “pure” correlation, e.g. all observed cases of “long” distributions, which can’t be approximated in a chosen way, are accompanied with change of IMF sectors. But according to the information, presented in Figure 1, we can conclude that all days of Full Moon and New Moon are characterised with increased intensity of thermal neutrons, so they are disturbed periods. Because increase is sufficiently essential, we can suppose distributions for these periods are “long”, so both Poison and logarithmically-normal functions must be used for their approximation. Certainly, this supposition must be tested using experimental data, where dates of Moon phases do not coincide with dates of the Earth’s crossings of IMF borders. This task is one of the most important purposes of our future research.
Studies of neutron counting rate distribution near the Earth crust have shown that:
References
Beliaeva, E.A., Kuzhevskij, B.M., Nechaev, O.Yu. Physical basis of a forecasting method for earthquakes and volcanos’ activity according observations of variations of neutron flux neat the Earth’s crust, Report at the IUGG-99 General Assembly, Birmingham, 1999(a).
Beliaeva, E.A., Kuzhevskij, B.M., Nechaev, O.Yu., Panasyuk, M.I. Neutron sources and nature of time variations of neutron flux near the Earth surface, Physical Ecology, Moscow
, №4, p.89, 1999(b).Kuzhevskij B.M. Nucleonics-based monitoring of the ecological environment balance of the Earth crust and lower atmosphere, 2000
Kuzhevskij B.M., et.al. Neutron field of the Earth, Origin and Dynamics, The Journal of the Korean Association for Radiation Protection, 2001, Vol.26, p.315.
Kuzhevskij B.M., et.al. The variations of neutrons’ concentration in thermal neutrons’ field of the Earth’s atmosphere, Preprint INP MSU 96-7/414.
Kuzhevskij B.M., Nechaev O.Yu., Sigaeva E.A. Seasonal dependence of thermal neutrons anisotropy near the Earth surface, 2002,
Vestnik MSU, Ser. Phys. & Astr., №1, p.101.

|